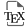no. 2
FFLV-type monomial bases for type B
Makhlin, Igor1
1 Skolkovo Institute of Science and Technology Center for Advanced Studies Ulitsa Nobelya 3 Moscow 121205 Russia and National Research University Higher School of Economics International Laboratory of Representation Theory and Mathematical Physics Ulitsa Usacheva 6 Moscow 119048 Russia
Algebraic Combinatorics, Tome 2 (2019) no. 2, pp. 305-322.

We present a combinatorial monomial basis (or, more precisely, a family of monomial bases) in every finite-dimensional irreducible 𝔰𝔬 2n+1 -module. These bases are in many ways similar to the FFLV bases for types A and C. They are also defined combinatorially via sums over Dyck paths in certain triangular grids. Our sums, however, involve weights depending on the length of the corresponding root. Accordingly, our bases also induce bases in certain degenerations of the modules but these degenerations are obtained not from the filtration by PBW degree but by a weighted version thereof.

Reçu le :
Révisé le :
Accepté le :
Publié le :
DOI : 10.5802/alco.41
Classification : 17B10, 17B20, 05E10
Mots clés : Lie algebras, type B, monomial bases, FFLV bases, FFLV polytopes, PBW degenerations
Makhlin, Igor 1

1 Skolkovo Institute of Science and Technology Center for Advanced Studies Ulitsa Nobelya 3 Moscow 121205 Russia and National Research University Higher School of Economics International Laboratory of Representation Theory and Mathematical Physics Ulitsa Usacheva 6 Moscow 119048 Russia 
@article{ALCO_2019__2_2_305_0,
     author = {Makhlin, Igor},
     title = {FFLV-type monomial bases for type $B$},
     journal = {Algebraic Combinatorics},
     pages = {305--322},
     publisher = {MathOA foundation},
     volume = {2},
     number = {2},
     year = {2019},
     doi = {10.5802/alco.41},
     mrnumber = {3934832},
     zbl = {07049527},
     language = {en},
     url = {http://www.numdam.org/articles/10.5802/alco.41/}
}
TY  - JOUR
AU  - Makhlin, Igor
TI  - FFLV-type monomial bases for type $B$
JO  - Algebraic Combinatorics
PY  - 2019
SP  - 305
EP  - 322
VL  - 2
IS  - 2
PB  - MathOA foundation
UR  - http://www.numdam.org/articles/10.5802/alco.41/
DO  - 10.5802/alco.41
LA  - en
ID  - ALCO_2019__2_2_305_0
ER  - 
%0 Journal Article
%A Makhlin, Igor
%T FFLV-type monomial bases for type $B$
%J Algebraic Combinatorics
%D 2019
%P 305-322
%V 2
%N 2
%I MathOA foundation
%U http://www.numdam.org/articles/10.5802/alco.41/
%R 10.5802/alco.41
%G en
%F ALCO_2019__2_2_305_0
Makhlin, Igor. FFLV-type monomial bases for type $B$. Algebraic Combinatorics, Tome 2 (2019) no. 2, pp. 305-322. doi : 10.5802/alco.41. http://www.numdam.org/articles/10.5802/alco.41/

[1] Ardila, Federico; Bliem, Thomas; Salazar, Dido Gelfand–Tsetlin polytopes and Feigin–Fourier–Littelmann–Vinberg polytopes as marked poset polytopes, J. Comb. Theory, Ser. A, Volume 118 (2011) no. 8, pp. 2454-2462 | DOI | MR | Zbl

[2] Backhaus, Teodor; Kus, Deniz The PBW filtration and convex polytopes in type B, J. Pure Appl. Algebra, Volume 223 (2019) no. 1, pp. 245-276 | DOI | MR | Zbl

[3] Carter, Roger Lie Algebras of Finite and Affine Type, Cambridge Studies in Advanced Mathematics, 96, Cambridge University Press, 2005, xvii+632 pages | MR | Zbl

[4] Cerulli Irelli, Giovanni; Feigin, Evgeny; Reineke, Markus Quiver Grassmannians and degenerate flag varieties, Algebra Number Theory, Volume 6 (2012) no. 1, pp. 165-194 | DOI | MR | Zbl

[5] Cherednik, Ivan; Feigin, Evgeny Extremal part of the PBW-filtration and nonsymmetric Macdonald polynomials, Adv. Math., Volume 282 (2015), pp. 220-264 | DOI | MR | Zbl

[6] Feigin, Evgeny The PBW filtration, Represent. Theory, Volume 13 (2009), pp. 165-181 | DOI | MR | Zbl

[7] Feigin, Evgeny 𝔾 a M degeneration of flag varieties, Sel. Math., New Ser., Volume 18 (2012) no. 3, pp. 513-537 | DOI | MR | Zbl

[8] Feigin, Evgeny; Fourier, Ghislain; Littelmann, Peter PBW filtration and bases for irreducible modules in type A n , Transform. Groups, Volume 16 (2011) no. 1, pp. 71-89 | DOI | MR | Zbl

[9] Feigin, Evgeny; Fourier, Ghislain; Littelmann, Peter PBW-filtration and bases for symplectic Lie algebras, Int. Math. Res. Not., Volume 2011 (2011) no. 24, pp. 5760-5784 | DOI | MR | Zbl

[10] Feigin, Evgeny; Makhlin, Igor Vertices of FFLV polytopes, J. Algebr. Comb., Volume 45 (2017) no. 4, pp. 1083-1110 | DOI | MR | Zbl

[11] Fourier, Ghislain Marked poset polytopes: Minkowski sums, indecomposables, and unimodular equivalence, J. Pure Appl. Algebra, Volume 220 (2016) no. 2, pp. 606-620 | DOI | MR | Zbl

[12] Hague, Chuck Degenerate coordinate rings of flag varieties and Frobenius splitting, Sel. Math., New Ser., Volume 20 (2014) no. 3, pp. 823-838 | DOI | MR | Zbl

[13] Kiritchenko, Valentina Newton–Okounkov polytopes of flag varieties, Transform. Groups, Volume 22 (2017) no. 2, pp. 387-402 | DOI | MR | Zbl

[14] Kus, Deniz Realization of affine type A Kirillov–Reshetikhin crystals via polytopes, J. Comb. Theory, Ser. A, Volume 120 (2013) no. 8, pp. 2093-2117 | MR | Zbl

[15] Molev, Alexander Weight bases of Gelfand–Tsetlin type for representations of classical Lie algebras, J. Phys. A, Math. Gen., Volume 33 (1999) no. 22, pp. 4143-4168 | DOI | MR | Zbl

[16] Stanley, Richard P. Two poset polytopes, Discrete Comput. Geom., Volume 1 (1986), pp. 9-23 | DOI | MR | Zbl

[17] Vinberg, Èrnest On some canonical bases of representation spaces of simple Lie algebras (2005) (conference talk, Bielefeld)

Cité par Sources :